Stochastic Models of Signaling Complexes

 

 

This research project is performed in close cooperation with the Smith lab. We jointly work on modeling techniques and tools to support the modeling of signaling complexes.

 

For students:

This project offers a multitude of interesting research questions that may serve as a topic for a Phd, Master or Master’s project. Specific topics are provided upon request. Note that for interested Computer Science students, we do not(!) expect any previous expertise in biological modeling.

 

A brief motivation of the topic from a biology point of view:

 

The stochastic gating of voltage- and ligand-gated ion channels in biological membranes that is observed by single channel recording techniques is often modeled using discrete-state continuous-time Markov chains (CTMCs). While these single channel models can be relatively simple (e.g., two physicochemically distinct states) or complex (hundreds of states), most include only two conductance levels (closed and open). For example, a transition state diagram for a three-state calcium (Ca²⁺)-regulated channel activated by sequential binding of two Ca²⁺ions is given by

 

 

 

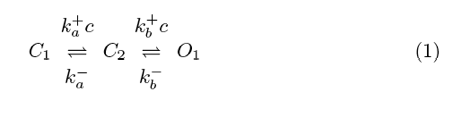
where k⁺_i c and k⁻_i with i ∈ {a, b} are transition rates with units of reciprocal time, k⁺_i is an association rate constant with units of conc⁻¹ time⁻¹, and c is the [Ca²⁺] near the channel. If this local [Ca²⁺] is specified, the transition-state diagram of the channel (1) defines a CTMC that takes on values in the state-space (C1, C2, O1). The experimentally observable conductance of this stochastically gating channel is the aggregated process of transitions between the closed and open classes of states: C = {C1, C2} and O = {O1}. The scientific literature developing stochastic models for the behavior of ion channels is largely focused on single channels or populations of independent channels. Notable exceptions are the work of Ball and colleagues analyzing interacting aggregated CTMC models of membrane patches containing several ion channels and the work by Smith et al. A second example are simulations of clusters of intracellular Ca²⁺-regulated Ca²⁺ channels inositol 1,4,5-trisphosphate receptors (IP3Rs) and ryanodine receptors (RyRs)—located on the surface of the endoplasmic reticulum or sarcoplasmic reticulum membrane—that give rise to localized intracellular [Ca²⁺] elevations known as Ca²⁺ puffs and sparks. When Markov chain models of Ca²⁺-regulated Ca²⁺ channels such as (1) are coupled via a mathematical representation of buffered diffusion of intracellular Ca²⁺, simulated Ca²⁺ release sites may exhibit the phenomenon of “stochastic Ca²⁺ excitability” where the IP3Rs or RyRs open and close in a concerted fashion (see Fig. 1 for representative simulation) .

 

 

 

 

 

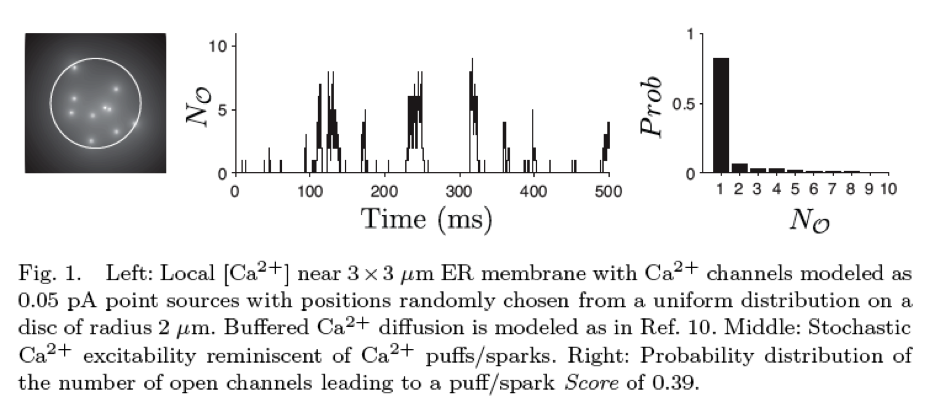
Such models are stochastic automata networks (SANs) that involve a large number of functional transitions, that is, the transition probabilities of one automata (i.e., an individual channel) may depend on the local [Ca²⁺] and thus the state of the other channels. The experimentally observable quantity is either the local [Ca²⁺] or the number of channels in the open class of states, N_O(t) (see Fig. 1, middle). The relationship between single channel kinetics of Ca²⁺-regulated channels and the emergent phenomenon of Ca²⁺ puffs and sparks is not well understood. However, if each release site configuration is known, several informative response measures can be determined from the steady-state probability distribution. For example, the so-called puff/spark Score given by Var[f_O]/E[f_O] is the index of dispersion of the steady-state fraction of open channels, f_O = N_O/N (see Fig. 1, right). This response measure takes values between 0 and 1, and a puff/spark Score of greater than approximately 0.3 indicates the presence of Ca²⁺ excitability. However, Ca²⁺ release sites are composed of 5–250 channels and this leads to a state-space explosion that makes numerical calculation of the stationary and transient distributions of model Ca²⁺ release sites challenging.

 

 

Publications

 

H. DeRimigio, P. Kemper, M.D. LaMar, G. Smith.

Markov chain models of coupled intracellular Calcium channels: Kronecker structured representations and benchmark stationary distribution calculations.

In: Proc. Pacific Symposium on Biocomputing 13:354-365(2008) (online proceedings),

a preliminary version appeared as Technical Report WM-CS-2007-06, College of William and Mary, June 2007.