Stochastic Workload Models for Storage Systems and Networks

 

 

Storage systems and networks are challenged with workloads that show burstiness, i.e., sudden peaks of demand that exceed average demand by far. Burstiness as expressed by self-similarity has been identified as an important traffic characteristic in computer systems and communication networks and has fueled much research in the networking community over the past decade. The performance implications of burstiness are considered dire and performance modeling must take burstiness, self-similarity, temporal dependencies adequately into account in its workload characteristics.

 

In this project, we will fully explore the abilities of Markovian Arrival Processes (MAPs), which so far have stimulated a lot of research in traffic modeling. MAPs can capture temporal dependance (thus burstiness) via the autocorrelation function. We believe that a MAP is the right and powerful mathematical tool to deal with burstiness in workload modeling and to turn the existing fundamental results into an applicable methodology with automated procedures that make workload modeling with MAPs truly applicable in practice. We target storage systems and networks as our systems under study and want to enhance MAPs in a way that synthetic workloads can be generated.

 

For students:

This project offers a multitude of interesting research questions that may serve as a topic for a Phd, Master or Master’s project. Specific topics are provided upon request.

 

Trace Data:

 

The SNIA IOTTA Repository is a collaborative effort sponsored by the Storage Networking Industry Association's Input/Output Traces, Tools, and Analysis Technical Work Group (IOTTA TWG). It provides free access to various kinds of measurement traces. For example, a sample trace from the set of MSR Cambridge traces show the following interarrival times for the first 500k requests for a particular disk (here: usr0). The unit of time is Windows Filetime.

 

 

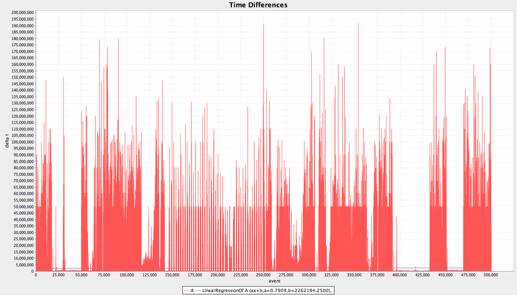
Obviously interarrival times differ by orders of magnitude and obviously there are particular patterns and phases a workload model should resemble.

If we partition interarrival times by orders of magnitude, we see that the empirical distribution is not trivial as the following diagram illustrates.

 

 

 

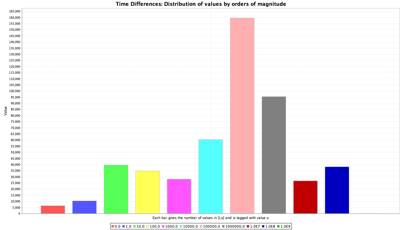
Much research has gone into techniques and tools to compute MAPs that are fitted to a particular trace and that match well its moments, joint moments or autocorrelation. However, more research is necessary to make MAPs fit not only with respect to time but also with respect to other characteristics like location, size and type of request.