![[*]](foot_motif.gif)
College of William and Mary
Christopher Siefert![[*]](foot_motif.gif)
College of William and
Mary
July, 2000
This is the manual for Release 0.4a of
the C++ implementation of Model-Assisted Pattern Search.
This document will hopefully get you on your feet when it comes to
executing this algorithm. It should
explain all you need to know about how to get this program to compile,
link and run successfully. The HTML version of this document was created
using LATEX2HTML. Since it is not perfect, there will be
mistakes in the html file. Read the postscript if you think the html is wrong. If you
have any questions at all, feel
free to email the author for a clarification.
This work is
was supported in part by a Batten Scholarship from the College of
William and Mary and by grants from the National Science Foundation
(CCR-9734044 and EIA-9712718).
Model-Assisted Pattern Search -- Release 0.4a
There are basically five categories of files that are included in the tarball. The first category contains the MAPS implementation files (which are discussed in Section 4). These contain the implementation for things unique to MAPS. Secondly, there are the Pattern Search files. They are versions of Dolan and Shepherd's Pattern Search implementation. These files are different from the ones found in the Pattern Search section of Virginia Torczon's software library, so don't expect those versions to compile with MAPS. Next we have the C. Siefert's Matrix and Vector class implementations, which are derived from R. Pozo's Template Numerical Toolkit. These are stock versions and are used `as-is'. They can be found at http://www.cs.wm.edu/~va/software/Vectors/. The fourth category includes S. Park's Lehmer pseudo-random number generation libraries and can be found at http://www.cs.wm.edu/~va/software/park/. The final category contains a few auxiliary utilities for maps which are also found on the maps web site; these are detailed in the appendices.
You'll also need a C++ compiler, that includes support for templates. This software was developed using egcs-g++ version 2.95.2.
tar zxvf maps.tgz
If your version of tar doesn't support the 'z' option (gtar does), then do the following:
gunzip maps.tgz (This will create maps.tar)
tar xvf maps.tar
If you downloaded netlibfiles.tgz, then install these libraries by running:
make install
This assumes that your version of tar supports the 'z' option. If not modify the Makefile to gunzip and then tar xvf. The next step is to compile and link the MAPS software. Do this by running:
make
For the trial run, you'll need an objective function. An implementation of a Shekel family function has been included. It should be automatically compiled by the Makefile.
If everything has succeeded up to this point, then you're all set for the example. If there was a problem, please refer to the Section 5.
cat sample.dat | ./maps
The second method involves answering a series of questions. They go as follows:
Welcome to the MAPS Test Program! Please provide the following information:
The prompts for the MAPS algorithm are listed below in order. Also listed are responses to those prompts for a trial run of MAPS.
Prompt
Response
Random Seed=
123456789
Number of Runs of MAPS=
1
Number of Variables=
4
Total Budget[V]=
20
Initial Design Budget[N] (less than total)=
10
Initial Mesh Size[Delta]=
0.01
Correlation Family(default=-1,EI=0,GI=1,EP=2,GP=3,CI=4)=
-1
Using default correlation...
Pattern Search(default=-1,Compass=0, MultiCompass=1)=
-1
Using default pattern search...
Assumed Trend (default=-1, Constant=0, Quadratic=1)=
-1
Using default trend...
Weighting Scheme(default=-1,WM=0,WTV=1,WDM=2,WDG=3,WD=4)=
-1
Using default weights...
Program name of function to optimize=
./shekel
Lower bound (space separated)=
0 0 0 0
Upper bound (space separated)=
10 10 10 10
Regardless of which method you used, the major section of the results should look something like this:
********** fn=./shekel V=20 N=10 Random seed=123456789 ******MAPS ITERATION HISTORY****** # for parameters V=20 N=10 P=4 delta=0.01 # on function: ./shekel NUM 1 2 3 4 VAL 1 0.11 3.14 5.51 5.09 -0.1371344 2 2.14 2.26 1.85 1.31 -0.34895367 3 7.5 6.63 3.94 0.67 -0.10299594 4 5.49 0.76 6.88 4.5 -0.12256296 5 9.65 4.03 4.15 8.32 -0.11180869 6 3.65 5.32 9.17 7.37 -0.14660693 7 8.67 9.78 0.72 6.78 -0.078442401 8 6.07 1.43 8.51 9.36 -0.082282933 9 4.81 8.22 7.62 3.94 -0.17825804 10 1.08 7.3 2.31 2.03 -0.12213042 11 2.15 2.26 1.85 1.31 -0.34759741 12 2.03 2.26 1.85 1.31 -0.36410903 13 1.48 2.26 1.85 1.31 -0.43621371 14 0.96 2.26 1.85 1.31 -0.45991384 15 1.05 2.26 1.85 1.31 -0.46101096 16 1.04 2.26 1.85 1.31 -0.46100608 17 1.06 2.26 1.85 1.31 -0.46098669 18 1.05 2.25 1.85 1.31 -0.46463045 19 1.05 2.24 1.85 1.31 -0.4682923 20 1.05 1.13 1.85 1.31 -1.0288096 Best Point found is #20, value=-1.0288096 **********************************
Your results need not be the same as those listed above. Indeed, due to differences in architectures, operating systems and compilers, it is unlikely that your results will be exactly like those listed above. At this point, you're set to run MAPS on your own problems. Refer to section 3.1 for information on how to use your own objective functions with MAPS.
The term ``fork-exec paradigm'' refers to the way UNIX and UNIX-like operating systems handle spawning another process. When MAPS wishes to evaluate a function, it forks or spawns off child process, and execs or runs your program as that process. MAPS then sends the program the point it wishes to evaluate the function at on its standard input. Your program should return the function value at that point on its standard output. If your program outputs anything else to its standard output, MAPS will probably crash. This is because of the method by which MAPS is communicating with your program. Consider yourself warned. If the function evaluation succeeds at a given point, MAPS expects your program to return zero. Likewise if evaluation fails, MAPS expects a non-zero return value. Included in Appendix C is a sample C++ objective function, that fits these specifications.
When specifying the function name for MAPS, it is important to make sure that either (1) the program is in a directory in your path or (2) that you specify a full or relative (./ etc.) path name. If you don't, chances are MAPS won't find your program.
One minor flaw of this current implementation is that it doesn't directly support objective functions with command-line parameters. If your program does require parameters, it is fairly trivial to write a shell script to ``wrapper'' it, so that MAPS can function properly. Appendix D has a sample script for this precise purpose.
The program you see running when you run maps is actually the testMPG test program for MAPS (see Appendix B for more information). Customizing the test program itself is dealt with in Section 3.4. For now we'll assume that your running the program 'as-is'. Prompts for input will come up in the following order. Items preceded by three asterisks (***) are options depending on your previous choices.
Random Seed=
You'll need to enter a seed for the random number generator, in order to generate the initial design for the problem. Any fairly large seed should work fine -- just remember what the seed is, in case you need to reproduce the results.
Number of Runs of MAPS=
If you're just trying to run the problem through MAPS to get an answer, enter one here. Otherwise, if you want to see the results of more than one MAPS run on the problem (for algorithm analysis, perhaps), enter the appropriate higher value here.
Number of Variables=
This is the number of variables your optimization problem has.
Total Budget[V]=
This is the number of function evaluations you're willing to allot MAPS to optimize the function.
Initial Design Budget[N] (less than total)=
This is the number of function values you want to allocate the initial design for MAPS. If you're not sure, use about a third to a half of the total budget.
Initial Mesh Size[Delta]=
This is the resolution to use for the initial mesh for MAPS. The best thing to do is to keep it about one-hundredth the size of the smallest variable space, or smaller.
Correlation Family(default=-1,EI=0,GI=1,EP=2,GP=3,CI=4)=
This option lets you choose which correlation family to use for the kriging in the MAPS algorithm. If you don't know (or have no preference), just use the default (which is Gaussian Isotropic). The other options stand for Exponential Isotropic(EI), Gaussian Isotropic(GI), Exponential Product(EP), Gaussian Product(GP) and Cubic Isotropic(CI). These correlations are not created equal, so change from the default only if you really know what you are doing. Section 4.7 lists the formulas for these functions.
Pattern Search(default=-1,Compass=0,MultiCompass=1)= ***MultiCompass Params(#searches,maxcalls,stream)=
Since MAPS requires that the search criterion be optimized, one of two types of pattern search are available for that purpose. The program defaults to a compass search. If you choose `MultiCompass,' which is a multi-started compass search, you will be given the option to choose three parameters for it. The first parameter is the number of searches to run, the second is the number of calls to let the compass search run for (-1 makes them run until convergence, which is the best option to use), and the last is the random stream. Be sure to use a number between 10 and 255 for the stream.
Assumed Trend (default=-1, Constant=0, Quadratic=1)=
At the moment, MAPS attempts to model the data from the objective function using either a constant (default) or a quadratic trend. Constant trend estimation should be suitable for most applications, but you might want to use the quadratic trend in certain cases (ie. if your objective function is vaguely quadratic).
Weighting Scheme(default=-1,WM=0,WTV=1,WDM=2,WDG=3,WD=4)=-1 ***Weighting Params (w_0,m)= ***Weighting Params (w_0,w_i,i%)= ***Weighting Params (w_0,dm)= ***Weighting Params (w_0,t%,m_b,m_g)= ***Weighting Params (w_0,m_b,m_g)=
The weighting scheme lets you choose the balance to strike between the accuracy of the approximation to your function and the desire to explore more fully the function space. The default setting uses a dynamic weighting scheme (Weight Dynamic) that compares the function value at the last evaluated point to its expected function value. If value compare favorably, then the weight on the approximation is increased. Likewise, if the values compare unfavorably, then the weight on the design criterion is increased. The default setting starts with a weight of w0=2.0, and multiplies it by mb=1.25 if the last value was ``bad'' and mg=0.75 if the last value was good. There are four other weighting schemes included in the current release of MAPS -- Weight Multiple(WM), Weight Target Value(WTV), Weight Delta Multiple(WDM) and Weight Dynamic Guess(WDG). The first weighting scheme lets you specify the initial weight w0, and a multiple m which is what the previous iteration's weight is multiplied by to yield the next iteration's weight. Weight Target Value lets you specify the initial weight w0, the weight of ``insignificance,'' wi, and the percent of the non-design function evaluations at which to reach the weight of insignificance. The Weight Delta Multiple scheme takes two parameters, the initial weight w0 and the multiple dm to multiply the weight by after a grid refinement. The Weight Dynamic Guess scheme is non-intuitive. You specify w0, a tolerance t, and two multiples mb for the ``bad'' multiplier, and mg for the ``good'' multiplier. If the last function value was within t% of the explored function value range of the approximation's expected function value at that point, then the current weight is multiplied by the ``good'' multiplier, else it is multiplied by the ``bad'' multiplier.
Program name of function to optimize=
The FULL PATH NAME of the program you wish to optimize. This means that you either have to include the entire path (e.g., /home/bob/func_26) or qualify the program name with a ./ signifying the current directory (e.g., ./func_26).
Lower bound (space separated)= Upper bound (space separated)=
These are the bounds of your problem, listed lower bounds first, each number separated by spaces and NOT by commas.
maps myobject;
Then one would refer to the RunSearch member function of the maps class as such:
myobject.RunSearch();
mp_vector best_point(Dim); /*Declares a Vector of size Dim*/ double best_value; /*Best value returned*/ maps mysearch(Budget,Dim,TheBounds,myfunc); /*Declares the maps class object*/ mysearch.RunSearch(); /*Runs the Search*/ mysearch.RetrieveBestSeen(&best_point, &best_value); /*Gets the best point, and best value seen. The `&' in this passes a pointer to the best_point and best_value objects. */
As a note, it is important to include the correct header files in your test program using the C/C++ #include compiler directive. The only files you need to include in a basic test program are maps_general.h and maps.h. If you are using a more advanced testing scheme, be sure to include the appropriate headers.
For the most part, in order to reset a particular parameter of MAPS, one creates an object with the desired characteristics, and then ``feeds'' it to the maps class object using the appropriate reset functions. This sort of model holds for making the appropriate settings for the Search Criterion, and other classes with class objects as members. For the following example, assume that we want to change from the default grid to another one that uses a special set of settings. First, we would create the new grid (a PSGrid class object) and set it appropriately, and then call the ResetGrid function of the maps class object. The following example illustrates this, assuming that a maps class object called mysearch has been declared, and that we wish to change its grid.
PSGrid newgrid; /*Declare the new grid*/ /*Here is where it is set with the special settings*/ mysearch.ResetGrid(newgrid); /*Changes the grid to the new grid*/
One particular change that one might desire to make, though it may not be immediately obvious how to do it, is changing the correlation function used for the parameter estimation for the kriging. In order to do this, one must create a special KrigApprox class object, ``feed'' that to a special SearchCriterion class object, and then ``feed'' that in turn to the maps class object. This is done in testMPG.cc (in Appendix B), and the following code is taken from it, assuming that DIM is the dimension of the space, COR is the number of the desired correlation function, and M is the maps class object.
maps M; /*Create the maps Object*/ KrigApprox KA(DIM); /*Create a KrigApprox Object*/ KA.ResetCorrelationFamily(COR); /*Set the Correlation Family*/ SearchCriterion SC(KA,b); /*Create the special Search Criterion*/ M.ResetSearchCriterion(SC); /*Modify MAPS*/
To use the testClassic interface, you create an objective function:
int mfcn(long DIM, double * x, double * f)
For this function, DIM is the dimension of the problem, x is a pointer to the evaluation site, and f is a pointer to the function value to be returned.
Then, in your program you have to give MAPS bounding information by calling:
void setbound(long DIM, double * lower, double * upper);
After setting the bounds, call MAPS using the function:
bool msearch(long DIM, double * initial_guess, long max_fevals, double tol);
If don't have a good guess for the initial starting point, send NULL in for initial_guess. Likewise, if you don't have a particular termination tolerance in mind, send in -1 for tol.
There one feature common to almost all of the classes listed below. These classes each have a debug(char*) function which outputs a near-complete picture of the state of the object at a given point in time. The string passed to debug, via the character pointer, will be output before each text line of its output.
MAPS has four different constructors, a default constructor, which does very little, a copy constructor and two special-purpose constructors. For most applications, the simpler special-purpose constructor of MAPS, will do a fine job. Its syntax is as follows:
maps(long V1, long P1, const Bounds &B1, char* fn)
The four parameters are (in order), the function evaluation budget, the dimension of the variable space, an object containing the bounds of the problem, and the name of the objective function (passed in as a character pointer). The more complicated special-purpose constructor allows the caller to completely set most of MAPS' initial state.
Like most other classes discussed below, the maps class also contains a collection of ``Reset'' functions, which allow for the caller to reset major state elements of MAPS before the search is run. They all have basically the same syntax, allowing the user to pass in some kind of object, and returning a bool indicating success or failure.
The RunMAPS function actually runs the Model-Assisted Pattern Search. It has one optional command-line parameter which is the name of the file prefix for iteration-by-iteration graphs of the Approximation and Search Criterion. Due to limits in visualization technology, this only works if your function has a one or two dimensional domain. These graphs are generated by the user-callable GenerateMAPSGraphics function, which can also be used to generate pictures of the final approximation and search criterion after RunMAPS has been called.
RetrieveBestSeen and GenerateIterationHistory are two other functions that allow the user to retrieve information following a successful run of MAPS. The former simply returns the best point and its value, whereas the latter outputs an 'iteration history' to standard output. A sample history is shown below:
******MAPS ITERATION HISTORY****** # for parameters V=14 N=5 P=2 delta=0.01 # on function: ./tk NUM 1 2 VAL 1 0.42 0.71 62.2503 2 0.67 0.33 42.6565 3 0.26 0.96 79.4194 4 0.87 0.08 177.17 5 0.73 0.41 34.4587 6 0.59 0.49 -6.39761 7 0.49 0.43 52.0737 8 0.63 0.57 63.6789 9 0.61 0.45 -58.9764 10 0.63 0.43 17.3618 11 0.57 0.43 40.8011 12 0.65 0.49 50.9157 13 0.61 0.47 -9.92294 14 0.49 0.53 60.0616 Best Point found is #9, value=-58.9764 **********************************
One can easily extract data from a file of these histories with use of system utilities such as grep, cut, and awk. Refer to Appendix B.3 for details on doing this.
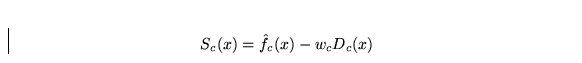
where Sc is the search criterion, ![]() is the current
approximation to the function, Dc is the design criterion, and
wc is the weight currently placed on the design criterion. The
approximation itself and design criterion are kept in an object of a
derived class of class Approximate, to which
SearchCriterion has a pointer.
is the current
approximation to the function, Dc is the design criterion, and
wc is the weight currently placed on the design criterion. The
approximation itself and design criterion are kept in an object of a
derived class of class Approximate, to which
SearchCriterion has a pointer.
Keeping track of the weighting scheme is the primary role for the SearchCriterion class. It currently has five types of weighting schemes. The first is called ``Weight Multiple,'' the second ``Weight Target Value,'' the third ``Delta Multiple,'' the fourth ``Dynamic Guess,'' and the fifth ``Dynamic.'' The first operates with a user specified starting weight, and a user specified multiple. During each iteration of MAPS, the current weight is multiplied by the weight multiple, to yield a new weight. The ``Weight Target Value'' scheme works off of a user-specified starting value, a user specified value of weight `insignificance' and a user specified iteration at which the weight is to become insignificant. The correct multiplier is then computed, and updates are handled much like in the ``Weight Multiple'' scheme. The ``Delta Multiple'' scheme works much like the ``Weight Multiple,'' except the weight is only reduced when delta is refined. The final two weighting schemes, ``Dynamic Guess'' and ``Dynamic'' both attempt to change the weight from from iteration to iteration depending on the current status of the approximation. The first uses a user-specified threshold percentage of the function range. The second uses a fixed distance of half the distance between the expected value at the last point and the best value as threshold. Experimentally, the final criterion (Dynamic) has shown the most promise.
In terms of interacting with the SearchCriterion class, the two most important functions are EvaluateSearchCriterion and UpdateSearchCriterion. They serve to allow MAPS to update and use the Search Criterion.
For the benefit of the user who may not be that familiar with this area of statistics, the following formulas represent the supported correlation functions:
Exponential Isotropic: 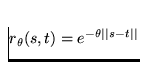
Gaussian Isotropic: 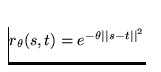
Exponential Product: 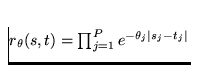
Gaussian Product: 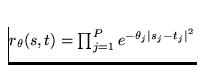
Cubic Isotropic: 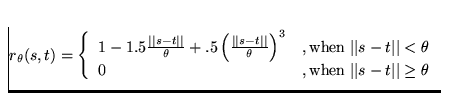
CC=gcc CXX=g++ FC=g77to:
CC=xlc CXX=xlC FC=xlf
vec.h:338: declaration of `operator >>' as non-function vec.h:338: parse error before `<' vec.h:338: declaration of `operator >>' as non-function vec.h:338: parse error before `<' cmat.h:397: declaration of `operator >>' as non-function cmat.h:397: parse error before `<'
Be sure to include the preprocessor macro OLD_LIBC. This error is due to the fact that your compiler doesn't fully support templates, but this problem is corrected easily through this macro. If you're using the makefile, add -DOLD_LIBC to the $(DFLAGS) line.
The compilation of MAPS will generate a number of warnings, but this is intended. There are class implementations that do not use all of their parameters, but the parameters are necessary for inheritance purposes. Hence, the compiler will probably spit out a warning, but this in no way detracts from the software's functionality.
The makefile is included for your benefit, and everything should work well. The makefile assumes that CLAPACK, BLAS, and the F2CLIBS are set up correctly as linkable libraries and are either in your library path or in the current directory. If you've changed the names or directory, edit the $(LDFLAGS) line in the makefile to reflect this. If your system administrator has installed these libraries system-wide, you should be fine so long as you get the names correct. If not, be sure to make the necessary changes in the makefile, or else MAPS won't link.
If it doesn't work, always remember to link from most general to least general. So for this program, link your files first, then MAPS, followed by CLAPACK, the CBLAS, the F2CLIBS, and finally the C math libraries.
Check to make sure you specified the dimension of the objective function correctly. If your objective function expects more variables that MAPS gives it, you'll probably hang the application.
Errors such as:
execlp: No such file or directoryare caused by incorrectly entering the name of the objective function. be sure to enter either a full (/home/user/program) or relative (./program) path for the program representing the objective function.
Cross-compilation is not an easy thing to do, and regardless of what kind of trick you use, it is bound to be system-dependent. Consult with your local compiler guru. Be careful to note the name-mangling done by all compilers involved.
Chances are this is a cross-compilation issue, and thus has to be dealt with accordingly. If it is not, be sure that you have a function called mfcn, which has the proper calling syntax.
Information on MAPS theory and results can be found in Model-Assisted Pattern Search (C. Siefert 2000). The full text of this document can be found in postscript form at: http://www.cs.wm.edu/~va/CS495#Chris.
awk -F mdat2tex.awk mydata.dat > myoutput.tex
The following is a the LATEX source for a sample table generated by mdat2tex:
% From file: sample.dat, this is table #0
\begin{center}\begin{tabular}{c|r|r|r|r|r}
\textbf{Iteration} &\textbf{$x_0$} &\textbf{$x_1$} &\textbf{$x_2$} &\textbf{$x_3
$} &\textbf{Value}\\
\hline
1& 9.8& 2.1& 4.2& 7.1& -0.192076\\
2& 2.8& 6.1& 6.7& 3.3& -0.351249\\
3& 1.5& 5.1& 2.6& 9.6& -0.249708\\
4& 6.3& 1.2& 8.7& 0.8& -0.49091\\
5& 7.1& 4.4& 9.9& 0.0& -0.22272\\
6& 6.7& 1.6& 8.7& 0.8& -0.566242\\
7& 7.1& 1.6& 9.1& 0.8& -0.544828\\
8& 6.9& 2& 8.7& 1.2& -0.586722\\
9& 7.1& 2& 8.3& 1& -0.700908\\
10& 7.7& 2& 7.7& 0.8& -0.838886\\
11& 7.7& 2& 7.1& 1& -0.775674\\
12& 8.1& 2& 7.7& 0.4& -0.720954\\
13& 7.7& 1.8& 7.7& 1& -0.986294\\
14& 7.9& 1.2& 7.7& 1.4& -1.30526\\
\end{tabular}\end{center}
\begin{center} Best Point is \#14, value=-1.30526
\end{center}
Run through LATEX, it looks like this:
| Iteration | x0 | x1 | x2 | x3 | Value |
|---|---|---|---|---|---|
| 1 | 9.8 | 2.1 | 4.2 | 7.1 | -0.192076 |
| 2 | 2.8 | 6.1 | 6.7 | 3.3 | -0.351249 |
| 3 | 1.5 | 5.1 | 2.6 | 9.6 | -0.249708 |
| 4 | 6.3 | 1.2 | 8.7 | 0.8 | -0.49091 |
| 5 | 7.1 | 4.4 | 9.9 | 0.0 | -0.22272 |
| 6 | 6.7 | 1.6 | 8.7 | 0.8 | -0.566242 |
| 7 | 7.1 | 1.6 | 9.1 | 0.8 | -0.544828 |
| 8 | 6.9 | 2 | 8.7 | 1.2 | -0.586722 |
| 9 | 7.1 | 2 | 8.3 | 1 | -0.700908 |
| 10 | 7.7 | 2 | 7.7 | 0.8 | -0.838886 |
| 11 | 7.7 | 2 | 7.1 | 1 | -0.775674 |
| 12 | 8.1 | 2 | 7.7 | 0.4 | -0.720954 |
| 13 | 7.7 | 1.8 | 7.7 | 1 | -0.986294 |
| 14 | 7.9 | 1.2 | 7.7 | 1.4 | -1.30526 |
gnuplot> plot "fpref.MAPS.GRAPH.dat" with lineswhere ``fpref'' is the file prefix you specify to testMPG, and ``GRAPH'' is either ``AP'' or ``SC'' depending on whether you want to view the approximation or search criterion graphs.
To produce plots for functions of two variables, type the following at the GNUplot prompt:
gnuplot> set parametric gnuplot> splot "fpref.MAPS.GRAPH.dat" with linesAgain, ``fpref' is the file prefix you specify to testMPG, and ``GRAPH'' is either ``AP'' or ``SC'' depending on whether you want to view the approximation or search criterion graphs.
Also, you can visualize the evaluation sites superimposed on either the approximation or the search criterion. To do so, type:
gnuplot> plot "fpref.MAPS.GRAPH.dat" with lines, "fpref.MAPS.PTS.dat" with pointsfor one variable functions. For two variable functions, type:
gunplot> set parametric gnuplot> splot "fpref.MAPS.GRAPH.dat" with lines, "fpref.MAPS.PTS.dat" with points
where ``fpref'' is the file prefix you specify to testMPG, and ``GRAPH'' is either ``AP'' or ``SC'' depending on whether you want to view the approximation or search criterion graphs.
cat mydata.dat | grep Best | cut -f2 -d=
If you want to see which iteration MAPS found the best point on for all of your trials, and want these numbers tallied, try:cat mydata.dat | grep Best | cut -f2 -d# | cut -f1 -d',' | sort -n | uniq -c
Or if you want to see the final fineness of the grid, and have this number tallied, try:
cat mydata.dat | grep delta | cut -f5 -d= | sort -n | uniq -c
#include <iostream.h>
int main() {
double x,y;
double f;
cin>>x>>y;
f=x+y;
cout<<f;
return 0;
}
Included with this distribution is a C++ program that implements the Shekel family of objective functions. The file shekel.cc, written by Erin Parker contains the implementation of this family of four-dimensional functions.
#!/bin/sh # Sample wrapper for a program with command-line arguments, # so it can work with MAPS # Chris Siefert, College of William and Mary my_objective_function arg1 arg2 arg3 exit $? # This returns the return value of the objective function
This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -no_navigation -show_section_numbers manual.tex.
The translation was initiated by Chris Siefert on 7/18/2000.
Virginia Torczon did some editing to remove unnecessary gifs
introduced by the translation and to add more active links on 5/15/2001.