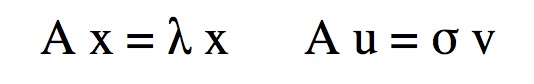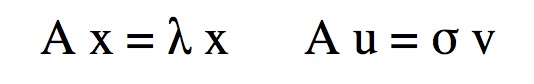PRIMME

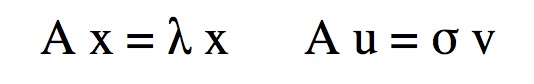PReconditioned Iterative MultiMethod Eigensolver

Version 3.2 (January 30, 2021)

Available at GitHub:

https://github.com/primme/primme

BSD license

The following two packages are PRIMME interfaces for Python and R users:
Repository pypi for Python
Repository CRAN for R

Documentation available in the distribution. Also here in pdf or HTML

A tutorial (presented at SIAM CSE 2017)

PRIMME is a C99 library to find a number of eigenvalues and their corresponding eigenvectors of a
Real Symmetric, or Complex Hermitian matrix A.
Generalized Hermitian Eigenvalue Problems are supported as of Version 3.0.
Singular values and their singular vectors of any square or rectangular matrix can also be computed (as of version 2.0).
Preconditioning and finding largest, smallest or interior eigenvalues/singular values is supported.
PRIMME is a multimethod eigensolver. Based on the Davidson/Jacobi-Davidson main iteration, it can transform to most known preconditioned eigensolvers by the appropriate choice of parameters. Preset methods are also provided, including the nearly optimal eigensolvers GD+k and JDQMR (see [1, 2]).
Under DYNAMIC method, the software alternates between DEFAULT_MIN_TIME and DEFAULT_MIN_MATVECS to estimate the parameters of a cost model, and identify the method that minimizes execution time for the given problem.
A multi-layer user interface allows efficient use by non-expert end-users, and a powerful experimentation testbed for eigenvalue research experts.
PRIMME is both parallel and sequential, based on an SPMD type of parallelization. In addition, multithreaded matrix-vector and BLAS libraries can be used.
PRIMME has many features such as blocking, locking, locally optimal restarting, and a host of others that make it extremely robust and efficient.
Full interface to MATLAB, Fortran77, Python, and,R.
The software has been tested extensively on a variety of architectures, systems, and applications.

Changes in Version 3.2

Fixed Intel 2021 compiler error "Unsupported combination of types for ."

Fixed compiling issues with PGI compiler also about tgmath.h.

Fixed dprimme() and other variants not returning error code PRIMME_MAIN_ITER_FAILURE when it should do in some corner cases.

Fixed warnings from gcc/clang undefined behavior sanitizers.

Matlab: renamed disp to reportLevel.

Matlab: add flag returnUnconverged to return unconverged pairs.

Matlab: return primme_params/primme_svds_params.

Changes in Version 3.1

Support for Generalized Hermitian Eigenvalue Problems.

Support for GPUs.

Support for multiple precisions (including half precision).

Dynamic memory allocation and modified interface.

Support for block orthogonalization for better CPU and parallel performance.

Blocked Jacobi-Davidson (solving all block equations simultaneously).

Added interface for Fortran 90.

Updated Python interface to Python version 3.8.

Added an optional callback for (parallel) broadcasting.

The callbacks can work with different precision than the main call (see "matrixMatvec_type" and "globalSumReal_type").

Added new counters: "numGlobalSum", "volumeGlobalSum", "numBroadcast", "volumeGlobalSum", "timeOrtho", "timeGlobalSum", "timeBroadcast".

Added "primme_params_create()", "primme_params_destroy()", "primme_svds_params_create()", and "primme_svds_params_destroy()".

Changes in Version 2.1

Improve threaded/parallel robustness by broadcasting the result of critical LAPACK operations instead of replicating them on every process.

Improved stopping criteria in QMR for interior problems.

MATLAB interface reimplementation with support for singular value problems, double or single precision, and compatible with Octave.

A full R interface as a CRAN package.

Proper reporting of convergence history for singular value solvers.

Various bug fixes and improved robustness.

Changes in Version 2.0

Changed license to BSD 3-clause.

New support for singular value problems.

New support for float and complex float arithmetic.

Support for problem dimensions larger than 2^31, without requiring BLAS and LAPACK compiled with 64-bits integers.

Improved robustness and performance for interior problems; implemented advanced refined and harmonic-Ritz extractions.

Python interface compatible with NumPy and SciPy Library.

Optional user-defined convergence function, convTestFun.

Several performance and robustness improvements

Changes in Version 1.2.2

Fixed wrong symbols in libdprimme.a and libzprimme.a.

primme_set_method sets JDQMR instead of JDQMR_ETol for preset methods DEFAULT_MIN_TIME and DYNAMIC when seeking interior values.

Fixed compilation of driver with a PETSc installation without HYPRE.

Included the content of the environment variable INCLUDE for compiling the driver.

Changes in Version 1.2.1

MATLAB interface to full PRIMME functionality.

Support for BLAS/LAPACK with 64bits integers (-DPRIMME_BLASINT_SIZE=64).

Simplified configuration of Make_flags and Make_links (removed TOP variable and replaced defines NUM_SUM and NUM_IBM by F77UNDERSCORE).

Replaced directories DTEST and ZTEST by TEST that has:
(a) driver.c: read matrices in MatrixMarket format and PETSc binary and call PRIMME with the parameters specified in a file; support complex arithmetic and MPI and can use PETSc preconditioners.
(b) ex*.c and ex*.f: small, didactic examples of usage in C and Fortran and in parallel (with PETSc).

Fixed a few minor bugs and improved documentation (especially the F77 interface).

Using Sphinx to manage documentation.

Changes in Version 1.2

Version 1.2 implements performance improvements and bug fixes that have been reported over the years by PRIMME's users, who the authors are indebted to.

A Fortran compiler is no longer required for building the PRIMME library. Fortran programs can still be linked to PRIMME's F77 interface.

Fixed some uncommon issues with the F77 interface

PRIMME can be called now multiple times from the same program.

Performance improvements in the QMR inner solver, especially for complex arithmetic

Fixed a couple of bugs with the locking functionality. In certain extreme cases where all eigenvalues of a matrix were needed. The order of selecting interior eigenvalues. The above fixes have improved robustness and performance.

PRIMME now assigns unique random seeds per parallel process for up to 4096^3 (140 trillion processes)

For the DYNAMIC method, fixed issues with initialization and synchronization decisions across multiple processes.

Fixed uncommon library interface bugs, coordinated better the set_method() and the user setting of parameters, and improved the interface in the sample programs and makefiles

Other performance and documentation improvements

Older versions are availabe at Github

Version 2.0 (Sep 20, 2016)
Version 1.2.2 (Oct 13, 2015)
Version 1.2.1 (Sep 7, 2015)
Version 1.2 (Dec 24, 2014)
Version 1.1 (October 2006)

Besides comments left on GitHub, consider contacting the developers with questions, bug reports, or requests.

Contact: ANDREAS at CS dot WM dot EDU

The following papers describe the research that has led to this software.
To cite PRIMME, please cite papers [1, 2]. Click for bibtex entries.

Development of Versions 1.2-2.0 were supported by National Science Foundation through grants CCF 1218349 and ACI SI2-SSE 1440700.
Current development is supported by NSF under NSCI 1835821 and under a DOE Exascale Computing Project 17-SC-20-SC.

Contributors:
James R. McCombs, Eloy Romero, Andreas Stathopoulos, Lingfei Wu

A. Stathopoulos and J. R. McCombs, PRIMME: PReconditioned Iterative MultiMethod Eigensolver: Methods and software description , ACM Transactions on Mathematical Software, Vol. 37, No. 2, (2010), 21:1--21:30.
L. Wu, E. Romero and A. Stathopoulos, PRIMME_SVDS: A High-Performance Preconditioned SVD Solver for Accurate Large-Scale Computations, SIAM J. Sci. Comput., Vol. 39, No. 5, (2017), S248--S271.
A. Stathopoulos, "Nearly optimal preconditioned methods for Hermitian eigenproblems under limited memory. Part I: Seeking one eigenvalue", SIAM J. Sci. Comput., Vol. 29, No. 2, (2007), 481--514. [ pdf ]
A. Stathopoulos and J. R. McCombs, "Nearly optimal preconditioned methods for Hermitian eigenproblems under limited memory. Part II: Seeking many eigenvalues", SIAM J. Sci. Comput., Vol. 29, No. 5, (2007), 2162-2188. [ pdf ]
L. Wu and A. Stathopoulos, "A Preconditioned Hybrid SVD Method for Computing Accurately Singular Triplets of Large Matrices", SIAM Journal on Scientific Computing 37-5 (2015), pp. S365-S388.
J. R. McCombs and A. Stathopoulos, "Iterative Validation of Eigensolvers: A Scheme for Improving the Reliability of Hermitian Eigenvalue Solvers", SIAM J. Sci. Comput., Vol. 28, No. 6, (2006), 2337--2358. [ pdf ]
A. Stathopoulos, "Locking issues for finding a large number of eigenvectors of Hermitian matrices", Tech Report: WM-CS-2005-09, July, 2005, submitted. [ pdf ]
A. Stathopoulos and K. Wu, "A block orthogonalization procedure with constant synchronization requirements", SIAM Journal on Scientific Computing, Volume 23, Number 6, (2002), 2165--2182. [ pdf ]
A. Stathopoulos "Some insights on restarting symmetric eigenvalue methods with Ritz and harmonic Ritz vectors", in Iterative Methods in Scientific Computation IV, D. R. Kincaid & Anne C. Elster (eds.), pp. 297--311, Series in Computational and Applied Mathematics, IMACS, NJ (1999). [ pdf ]
A. Stathopoulos and Y. Saad, "Restarting techniques for (Jacobi-)Davidson symmetric eigenvalue methods", special issue on eigenvalue methods, Electronic Transactions on Numerical Analysis, Vol. 7, (1998), 163-181.
K. Wu, Y. Saad and A. Stathopoulos, "Inexact Newton Preconditioning Techniques for Eigenvalue Problems", special issue on eigenvalue methods, Electronic Transactions on Numerical Analysis, Vol. 7, (1998), 202-214.
A. Stathopoulos, Y. Saad, and K. Wu, "Dynamic Thick Restarting of the Davidson, and the Implicitly Restarted Arnoldi Methods", SIAM J. Scientific Computing, 19, 1, (1998) 227-45. Copyright © 1998 Society for Industrial and Applied Mathematics. [ pdf ]
A. Stathopoulos, Y. Saad, and C. F. Fischer, "Robust Preconditioning of Large, Sparse, Symmetric Eigenvalue Problems," the Journal of Computational and Applied Mathematics, 64 (1995) 197-215. [ pdf ]
A. Stathopoulos and C. F. Fischer, "A Davidson Program for Finding a Few Selected Extreme Eigenpairs of a Large, Sparse, Real, Symmetric Matrix," Computer Physics Communications, 79 (1994) 268-290. [ pdf ]

Back to my home page